Discuss 2×2 factorial designs with relevant example.
This would be called a 2 x 2 (two-by-two) factorial design because there are two independent variables, each of which has two levels. If the first independent variable had three levels (not smiling, closed-mouth, smile, open-mouth smile), then it would be a 3 x 2 factorial design. Note that the number of distinct conditions formed by combining the levels of the
independent variables is always just the product of the numbers of levels. In a 2 x 2 design, there are four distinct conditions. In a 3 x 2 design, there are 6.
Layout of Factorial Design: The simplest case is what is called a 2 x 2 design.
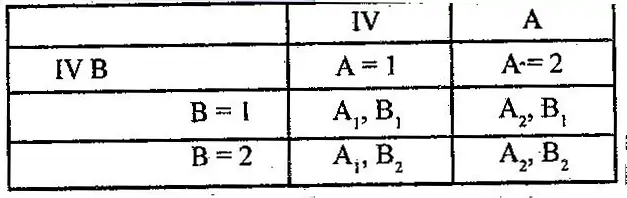
This is the simplest case of a two way design, each IV has two levels.
IV A has 1 and 2.
IVB has 1 and 2.
- There are 4 cells: A1B1, A1B2, A2B1, A2B2.
- This is a 2 x 2 design. 2 x 2 tells you a lot about the design.
- There are two numbers so there 2 IVs.
- The first number is a 2 so the first IV has 2 levels.
- The second number is a 2 so the second IV has 2 levels.
- 2 x 2= 4 and that is the number of cells A 2 x 3 design.
- There are two numbers so there 2 IVs.
- The first number is a 2 so the first IV has 2 levels.
- The second number is a 3 so the second IV has 3 levels.
- 2 x 3 = 6 and that is the number of cells.
Example of Factorial Design
The table below represents a 2 x 2 factorial design in which one independent variable is the type of psychotherapy used to treat a sample of depressed people (behavioural vs cognitive) and the other is the duration of that therapy (short vs long).
The dependent variable, which is not actually shown in this table is a measure of improvement.) Each cell in the table, therefore, represents one of the four distinct conditions, short behavioural therapy, short cognitive therapy, long behavioural therapy, and long cognitive therapy. Inside the cells, you can put different things.
In this example, it is the number of participants in each condition. (The symbol n generally refers to the number of subjects in a condition.) You could also put expected results or actual results (e.g., means and standard deviations) into the cells of the table if you wanted to.

In a factorial design, each independent variable can be manipulated between subjects or within subjects and this decision must be made separately for each one. In the design above, it makes sense that participants will receive only one kind of psychotherapy. They will receive either behavioral or cognitive, not both.
And they will receive either short or long, not both. That explains the “B”s in parentheses after each variable name they stand for “between subjects.” What this implies is that each participant will be in only one of the four distinct conditions.



